Инверзија

Аналитичка форма инверзије

* Разматрамо како инверзија изгледа аналитички и користећи добијени резултат доказаћемо још нека њена својства.

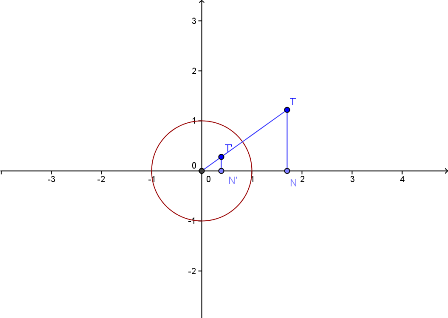
Нека је

Oxy

правоугли координатни систем у равни

Е^{2}

. Не умањујући општост посматраћемо инверзију у односу на јединични круг

k(0,1)

.
Нека су даље координате придружених тачака

T(x,y)

T'(x',y')

, а

N

N'

подножја нормала из

T

T'

на x-осу.
Из сличности троуглова △

ONT

и △

ON'T'

следи

y' : x' = y : x

.
Према дефиницији инверзије је

|ОТ|·|ОТ'| = 1

, односно координатно

(x^{2} + y^{2}) ·
	({x'}^{2} + {y'}^{2}) = 1

.
Решавањем овог система по x' и y' следи да је

$x' = \frac{x}{x^{2} + y^{2}}$ , $y' = \frac{y}{x^{2} + y^{2}}$ .

Дакле, инверзија

ψ_{k}

описана је формулама

$ψ_{k} :
(x,y)
→
(x',y')=
(\frac{x}{x^{2} + y^{2}}, \frac{y}{x^{2} + y^{2}}).$

Aко бисмо изразили

x

y

помоћу

x'

y'

добили бисмо

$x = \frac{x'}{{x'}^{2} + {y'}^{2}}$ , $y = \frac{y'}{{x'}^{2} + {y'}^{2}}$ .

Oво је у складу са чињеницом да је инверзија инволутивна трансформација.
Истакнимо такође да из претходне формуле добијамо да је инверзија бијекција на скупу

Е^{2} /{O}

. Користећи ове формуле можемо доказати сва до сад наведена својства инверзије, као и једно од основних својства инверзије, а то је да инверзија чува углове али мења оријентацију.

* Пример

Нека је

k

круг инверзије и

p

права која сече

k

, али не садржи њен центар

О

, тада је

p'

кружница кроз

О

. Доказаћемо да је средиште те кружнице

p'

тачка симетрична тачки

О

у односу на праву

p

.
Решење:

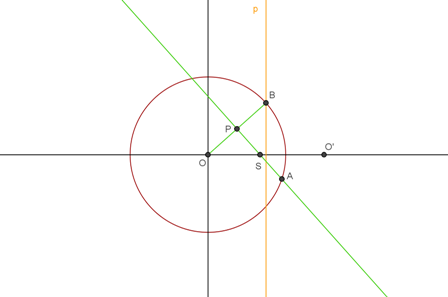
Одаберемо координатни систем као на слици. Нека

p

има једначину

x=a,   0 < a < r

и нека је

k(0,1)

. Тада је

O'=(2a,0)

. Нека је

S

инверзна слика од

O'

, тада она има координате

S=(\frac{1}{2a},0)

. Задатак ће бити доказан ако покажемо да симетрала дужи

OB

сече праву

p

управо у тачки

S

. Најпре средиште

P

од

OB

има координате

P=(\frac{a}{2}, \frac{\sqrt{1 - a^{2}}}{2})

. Симетрала те дужи

OB

има једначину

y - \frac{\sqrt{1 - a^{2}}}{2} = - \frac{a · (x - \frac{a}{2})}{\sqrt{1 - a^{2}}}

.
Пресек

x

- осе и симетрале дужи

OB

задовољава једнакост

- \frac{\sqrt{1 - a^{2}}}{2} = - \frac{a · (x - \frac{a}{2})}{\sqrt{1 - a^{2}}}

.
Одавде је

x= \frac{1}{2a}

, па је тврдња доказана.